meta: I expanded my notes (bold) into a more consumable format with an editorialized output of a language model.

let’s talk about natural selection via the lens of evolutionary algorithms.

In an evolutionary algorithm, a set of candidate solutions (called “individuals” or “genomes”) is generated and then evaluated according to a set of criteria (called the “fitness function”). The individuals with the highest fitness are then selected to “reproduce” and create new, slightly modified versions of themselves (called “offspring”). This process is repeated over many generations, with the fittest individuals being selected for reproduction each time. Over time, this can lead to the evolution of increasingly fit solutions to the given problem.

reducing you search spaces orders of magnitude does not in itself help, if your original search space was surastronomical to begin with.

Reducing the search space of an algorithm can help to make it more efficient by limiting the number of possible solutions that need to be considered. This can save computational resources and make it possible to find a solution more quickly. However, if the original search space is already very large, then reducing it by even an order of magnitude may still not make the algorithm practical to use. In such cases, it may be necessary to use other techniques, such as parallelization or approximate algorithms, to make the problem tractable.

Additionally, it’s important to consider whether the reduced search space is still representative of the original problem. If the search space is reduced too much, it may not contain any solutions that are relevant to the original problem, in which case the algorithm may not be useful.

size of search space, therefore, isn’t everything if your evaluation function isn’t right. in fact, a good evaluation function might be just the key design aspect of your algorithm. it’s advantageous to build in milestones in natural search.

A well-designed evaluation function is crucial for ensuring that the algorithm is able to find good solutions to the given problem. If the evaluation function is not accurate or comprehensive, then the algorithm may not be able to identify the fittest solutions, which can lead to suboptimal results. On the other hand, a good evaluation function can help to guide the algorithm towards the best solutions, improving its efficiency and effectiveness.

Building check points into the natural search process can also be useful for improving the efficiency of the algorithm. By periodically evaluating the current state of the search and adjusting the search parameters accordingly, it can be possible to guide the algorithm towards better solutions and avoid getting stuck in local optima.

when we attempt to formalize the search space for a goal we have in mind, we can compromise. as we established, blindly reducing search space isn’t generally optimal. our search space is defined in conjunction with other design choices, such as the aforementioned evaluation function.

When formalizing the search space for a particular goal, it is important to consider the trade-offs between different design choices. For example, reducing the search space may make the algorithm more efficient, but it may also limit the possible solutions that can be found.

we have power over the means of information propagation, ie. what “is” a solution. the environment (evaluation function) has its set of rules, and an individual (solution) defines how to chain those rules to reach some state (e.g. replication). the solution is the domain and the state is the range of the evaluation function.

In the context of evolutionary algorithms, the evaluation function plays a key role in determining which solutions are considered “fit” and therefore eligible for reproduction. The evaluation function defines the rules that solutions must follow in order to be considered successful, and it determines the “fitness” of each solution based on how well it follows those rules.

The solutions, or individuals, can be thought of as the domain of the evaluation function, and the fitness values that are assigned to them can be thought of as the range. The goal of the evolutionary algorithm is to find solutions that are able to “chain together” the rules defined by the evaluation function in order to reach a high fitness value, or a desirable state.

if a complex solution is needed, such as the human brain, it’s more efficient to compress it into a blueprint that can be bred. one can appreciate a programmable format such as the DNA. this requires another set of rules which translates the compressed information into a solution.

It can be more efficient to represent complex solutions in a compressed or encoded form that can be manipulated and evolved using an algorithm. This is often the case for solutions that are too large or complex to be represented directly, such as the human brain.

One way to do this is to use a programmable format, such as DNA, which can encode information in a compact and manipulable form. DNA is a sequence of nucleotides that carries genetic information, and it can be used to encode solutions to complex problems. By representing solutions in this form, it becomes possible to apply evolutionary algorithms to search for better solutions by breeding and mutating the encoded information.

However, this requires another set of rules to translate the encoded information into a solution. These rules define how the encoded information is decoded and used to generate a solution to the given problem.

for a bullet point summary: we can think in terms of the following degrees of freedom when it comes to definitions of

• evaluation function (environment)
• solution (individual)
• compression (genetic instructions)
• decompression (gestation)
• selection (mate selection)
• recombination (fertilisation)

Here is a summary of the key points we discussed:

• The evaluation function, also known as the environment, defines the rules that solutions must follow in order to be considered “fit” and eligible for reproduction.
• The solutions, or individuals, are the inputs to the evaluation function, and the fitness values that are assigned to them are the outputs.
• The process of natural selection is simulated using evolutionary algorithms, which mimic the process of reproduction and selection in order to find good solutions to a given problem.
• In order to make the problem tractable, it may be necessary to represent complex solutions in a compressed or encoded form that can be manipulated and evolved using an algorithm.
• This requires another set of rules, known as the decoding rules, to translate the encoded information into a solution. These rules define the virtual environment in which the solutions encoded in DNA can be evaluated and evolved.

now let’s assume that we want a solution which is able to learn and interpret patterns and produce new ones. we want intelligence. let’s make some conjectures about what would improve the odds of an appearingly intelligent solution in the context of evolutionary algorithms.

a network is a safe bet. nodes operate with a limited information, process it and forward it to other nodes. there are two primary objects in a network: a node and a connections. therefore, our compressed artifact defines what are the nodes and how they send information. there are two distinct instruction sets interpreted by the decompression function to build the solution: hodology and computation the network can be built as a tree from a root.

Using a network of interconnected nodes is a good approach for generating solutions that are able to learn and interpret patterns. In a network, each node operates on a limited amount of information, processes it, and then forwards it to other nodes. This allows the network to distribute the workload and make use of parallel processing, which can make it more efficient and effective at solving complex problems.

In a network-based solution, there are two primary objects that need to be defined: the nodes and the connections between them. The compressed artifact that encodes the solution therefore needs to define what the nodes are and how they send information to each other. This can be done using a programmable format, such as DNA, which can encode the instructions for building the network in a compact and manipulable form.

The process of decompressing and interpreting the encoded instructions is performed by the decompression function. This function uses two distinct instruction sets to build the solution: one set for defining the nodes, and another set for defining the connections between them. By combining these instruction sets, the decompression function can build a network of interconnected nodes that is capable of solving the given problem.

what are some useful chainable instructions?

an instruction for branching creates new leaves. a branching instruction creates a new leaf, which has an independent pointer to the genome, and can therefore build independent structures.

duplication is exponential and we observe it everywhere in nature. a duplication instruction has one parameter: how deep (how many branches) back to go to duplicate the structure.

some sort of penalty for length of genome should be introduced to encourage duplication of useful structures rather than using too many branching instructions.

Some useful chainable instructions in an evolutionary algorithm might include branching, duplication.

Branching instructions can be thought of as similar to cell division in biology. Cell division allows an organism to grow and develop new structures.

Duplication instructions allow the algorithm to reuse existing solutions and build upon them, rather than starting from scratch each time. This can help to avoid redundant work and improve the efficiency of the algorithm.

now that we’ve built a node graph with some rudimentary connections, we define richer hodology. nodes have markers that define afferent areas. given the expected size of the network, they ought to be combined with probabilities.

Once a node graph has been created with some basic connections, it is possible to define a more complex hodology for the network. This can be done by assigning markers to the nodes that define their afferent areas, or the areas from which they receive input.

Given the expected size of the network, it may be useful to combine these markers with probabilities to more accurately reflect the likelihood of different connections being made.

how to decide which markers connect to which?

0 16 16 48 80
1 15 17 47 81
...
7 09 23 41 87
8 08 24 40 88
/ // 25 39 89
/ // 26 38 90
...
/ // 31 33 95
/ // 32 32 96

a complement system. the closer two markers are to a power of two, the higher chance of a connection from lower to higher marker. the magnitude of the smaller marker determines the span, ie. smaller numbers are used for more local connections.

One approach to deciding which markers should connect to which in an evolutionary algorithm is to use a complement system. In this approach, the closer two markers are to a power of two, the higher the likelihood of a connection being made from the lower marker to the higher marker. Additionally, the magnitude of the markers can be used to determine their span, with small numbers being used for local connections and larger numbers being used for more global connections.

let’s divorce the concept of a node as a computational unit from the concept of a node as a network building unit. a single node can contain many neurons (computational units.) an instruction to create a neuron in the current node takes three parameters: type of neuron, a marker and quantity in some probabilistic notation. the type of a neuron is going to be an index in some sort of table that contains the instructions for setting up a neuron. (the other instruction set mentioned earlier.)

An instruction to create a neuron in the current node would take three parameters: the type of neuron, the marker for the neuron, and the quantity of neurons to be created. The type of neuron would be an index in a table that contains the instructions for setting up the neuron, while the marker would provide additional information and context about the neuron and its connections.

This approach allows for greater flexibility and customization in the design of the network, as different types of neurons can be created and assigned to different nodes based on the specific goals and requirements of the algorithm. It can also help to improve the performance of the algorithm by allowing for more precise control over the structure and function of the network.

let’s summarize the instructions so far.

1. BR(anch)
2. DUP(licate) #depth
3. N(eu)R(on) #type #marker #quantity

for example, this genetic sequence generates the following network (note that the parameters are simplified for illustrative purposes.)

BR NR(red, 14, 2) NR(blue, 2, 3) BR NR(green, 14, 2)

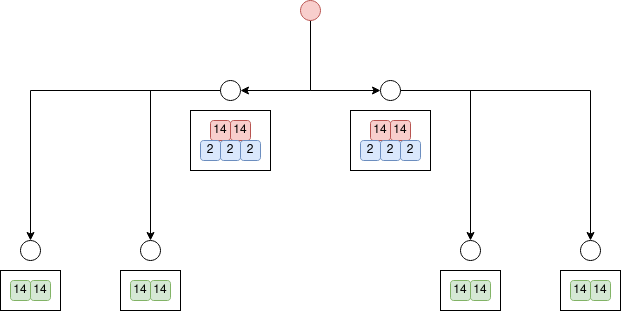
say we extend the above sequence with instruction DUP(1)

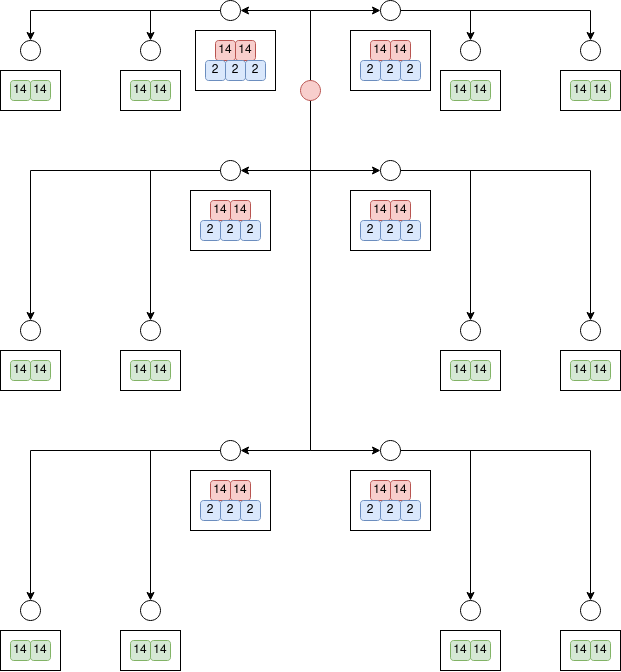
the duplication instruction was done four times, because there were four active leaves at the time of executing it. let’s add another instruction which probabilistically terminates an active leaf: END #probability

an individual needs to receive inputs and outputs from the environment. the inputs and outputs will vary greatly as the evaluation function is iterated. initially, the solutions solve simple logical gates. then, continuous variables are introduced and combined with the binary inputs. the complexity of inputs and outputs increases.

In order for an individual in an evolutionary algorithm to be effective, it must be able to receive inputs and outputs from the environment. The nature of these inputs and outputs will vary depending on the specific goals and requirements of the algorithm, as well as the progress of the search.

Initially, the solutions generated by the algorithm may be designed to solve simple logical gates. As the search progresses and the evaluation function is iterated, the complexity of the inputs and outputs may increase, incorporating continuous variables and more complex combinations of binary inputs.

By allowing the complexity of the inputs and outputs to increase over time, it is possible to gradually improve the performance of the algorithm and find increasingly high-quality solutions to the given problem. This can help to make the algorithm more versatile and effective, allowing it to solve a wider range of problems.

a neuron can have multiple markers. there exist special markers which define environment inputs and outputs. how does the evaluation function read outputs from neurons is going to be proposed when we enter the discussion about an instruction set for building a neuron.

there are two opportunities with respect to mutations: instructions and their parameters. additionally, a mutation can be continuous or reconstructive.

The evaluation function would need to be able to read the output signals from the axon in order to assess the neuron’s performance. This would typically involve measuring the strength and timing of the signals that are transmitted by the neuron, as well as any other relevant characteristics. The specific details of how this would be done would depend on the specific instruction set used to build the neuron and the particular problem being solved.

the compressed genetic sequence only describes how to build a network. a design of a neuron’s genetic sequence must take into account the fact that this network, once constructed, still needs to learn the patterns exposed by the environment. this smells like a huge computational bottleneck.

The compressed genetic sequence is a hypothetical set of instructions that describes how to build a network of neurons. It is a theoretical concept that is used to illustrate how the structure and function of the nervous system could be encoded in a genetic sequence.

While the compressed genetic sequence may provide a general blueprint for constructing a network of neurons, it does not provide any information about how the network should learn and adapt to the patterns and stimuli in the environment. In order for the network to be able to learn and adapt, it must be exposed to a variety of input signals and be able to modify its connections and response patterns accordingly.

This learning process is a critical aspect of the functioning of the nervous system, but it can also be a computational bottleneck.

issue: small change in the order of instructions results in drastically different solutions. DNA has redundancy and the genetic information between mates is largely the same. useless information is graciously lost due to destructive nature of mutations. more graciousness and resilience can be introduced over two dimensions: probabilistic building and redundancy.

One potential issue is that small changes in the order of instructions can result in drastically different solutions. This is because the instructions in a solution’s DNA are executed sequentially, and small changes in the order of instructions can lead to large changes in the resulting solution.

One way to address this issue is to introduce more redundancy into the solutions’ DNA. This means including multiple copies of the same instructions in different parts of the DNA, so that the solution can still function correctly even if the order of instructions is changed.

Another way to address this issue is to use probabilistic building in the decompression function. This means allowing the function to randomly choose between different possible instructions at each step, rather than executing the instructions in the DNA in a fixed order. This can help to make the solutions more resilient to changes in the order of instructions.

cell DNA determines what proteins are created and their concentrations. the concentrations are the deciding factor in the cells behavior. the decompression should keep state resembling protein concentrations in the leaves. these concentrations then affect what instructions are selected next.

The DNA of a cell determines what proteins are created and their concentrations. The concentrations of these proteins are the key factor in determining the behavior of the cell.

The decompression function could use the protein concentrations to determine which instructions are most likely to be selected at each step. This could be done by assigning probabilities to different instructions based on the protein concentrations, with instructions that are more likely to be selected given higher protein concentrations.

let’s remove the duplication instruction. a change in its parameter is too destructive and non-continuous. the behavior is reachable with branching. the branching instruction is strictly constructive.

Branching instructions are strictly constructive, meaning that they only add new, independent structures to the solution, whereas duplication instructions can be destructive and non-continuous, resulting in drastic changes to the solution.

However, it’s important to note that duplication instructions can be useful in some cases, as they can help to create more efficient solutions by allowing the reuse of existing structures.

before we define the concentration state we need to design how does it select instructions. to make progress there, a proposal for reuse of structures is needed. this is fundamental. how do we select scope of structures (chains of instructions) and how do we refer to them?

One way to select instructions in an evolutionary algorithm is to use a mechanism that allows for the reuse of structures. This means allowing the algorithm to refer to existing structures, rather than requiring it to build new structures from scratch at each step.

To do this, you will need to design a mechanism for selecting the scope of structures (i.e. which chains of instructions will be considered for reuse) and for referring to these structures in the instructions. For example, you could use a system of labels and pointers to identify and refer to specific structures.

… to be continued …