Environment sniffing with localizers
In his novel A Deepness in the Sky Vernor Vinge describes a nano technology called “the localizers.” These point-sized objects float in zero-gee and communicate with other localizers in their proximity. A localizer is equipped with some processing power and sensors.
Localizers in zero-gee are a handy abstraction for thinking about distributed systems. They can model systems across scales (a point can be a dust smite or a planet) and one can plug in any interesting sensors and constrains.
A hello world setup is a confined 3-space $S$ of $V_s = 1$ in which localizers are represented by a single point. A localizer can detect the number of peers in its proximity at distance $r = 0.000001$. A million localizers uniformly distributed in $S$ give us ~6 detectable peers. Localizers are pushed away by solid objects we send through the space.
For example, a ball moves across $S$ and we simulate the displacement of localizers in its way. We control 3 localizers $C = \set{c_0, c_1, c_2}$, called controllers, at one of the faces of $S$. How do we leverage the network to track the movement of the ball?
Displacement detection
Consider the following algorithm:
A localizer broadcasts a message ANOMALY to its peer if the number of its
peers rapidly changes. ANOMALY message contains two parameters:
ORIGINis an identifier of the localizer;HOPSis a counter of hops this message has travelled, set to 0.
When a localizer receives ANOMALY message, it relays it with the same
ORIGIN parameter and the HOPS parameter incremented by 1.
Clearly the above algorithm leads to infinite cycles. To patch this defect we
store a set $O$ of recently relayed ORIGINs. A localizer ignores messages
with their ORIGIN in $O$. A message which started in a single localizer now
expands like a shock wave through the network, eventually hitting $C$. Since we
know the size of $S$, HOPS parameter estimates distance1. We need to
receive a message from the same ORIGIN on all 3 controllers to have some
certainty about the origin of the message2.
I propose an experiment in which some RL agent has access to the messages received by the controllers. We simulate a ball moving randomly in $S$. The agent must estimate the center of the ball assuming that the speed of the message passing is orders of magnitude faster than the speed of the ball.
Querying the network
Instead of displacement, localizers can broadcast sensory data. An operator of such network might want to make queries to the network rather than passively await an anomaly. For example, let’s assume that the localizers are equipped with thermometers and the operator wants to measure the temperature around some point $P$. We need to solve two problems:
- How to read the temperature only from localizers around $P$ in $S$? Can we generalize into more complex spaces?
- How to target the query and deliver an answer with a minimal bandwidth usage?
Let’s start with a simple case where we know the localizer density of $S$, localizers are uniformly distributed and we broadcast messages from one receiver in all directions (shock wave shape) with approximately equal speed.
Consider the following algorithm:
The controllers emit QUERY message with following parameters:
HOPS_TO_GOis an integer decremented with each relay. A localizer which decrements this parameter to 0 stops relaying the message and stores it in memory instead (for some short period of time $T$).GIDis an identifier which allows us to have multiple independent parallel queries in the network.UNIONin an integer which dictates the minimum count ofQUERYmessages with the sameGIDwhich must arrive within $T$ and decrementHOPS_TO_GOto 0 in order for the localizer to answer the query.
We can interpret HOPS_TO_GO as a distance from a controller to the localizers
in the area we want to query. But since the message propagates like a shock
wave, the HOPS_TO_GO “distance” is a radius around the controllers. We
therefore combine messages from several controllers and target the intersection
of their shock waves with the UNION parameter.
Let’s introduce a static obstacle $O$, a cube of $V_O = 0.25$ in the center of $S$. We have perfect knowledge of the environment, however we cannot rely on the translation between hops and distance beyond $O$.
We introduce a forth parameter TAIL to the QUERY message. TAIL parameter
contains another QUERY message. The recursive nature of TAIL works like a
schedule. Following figures depict how this concept works in a 2-space with 2
initial controllers $S_1$ and $S_2$.
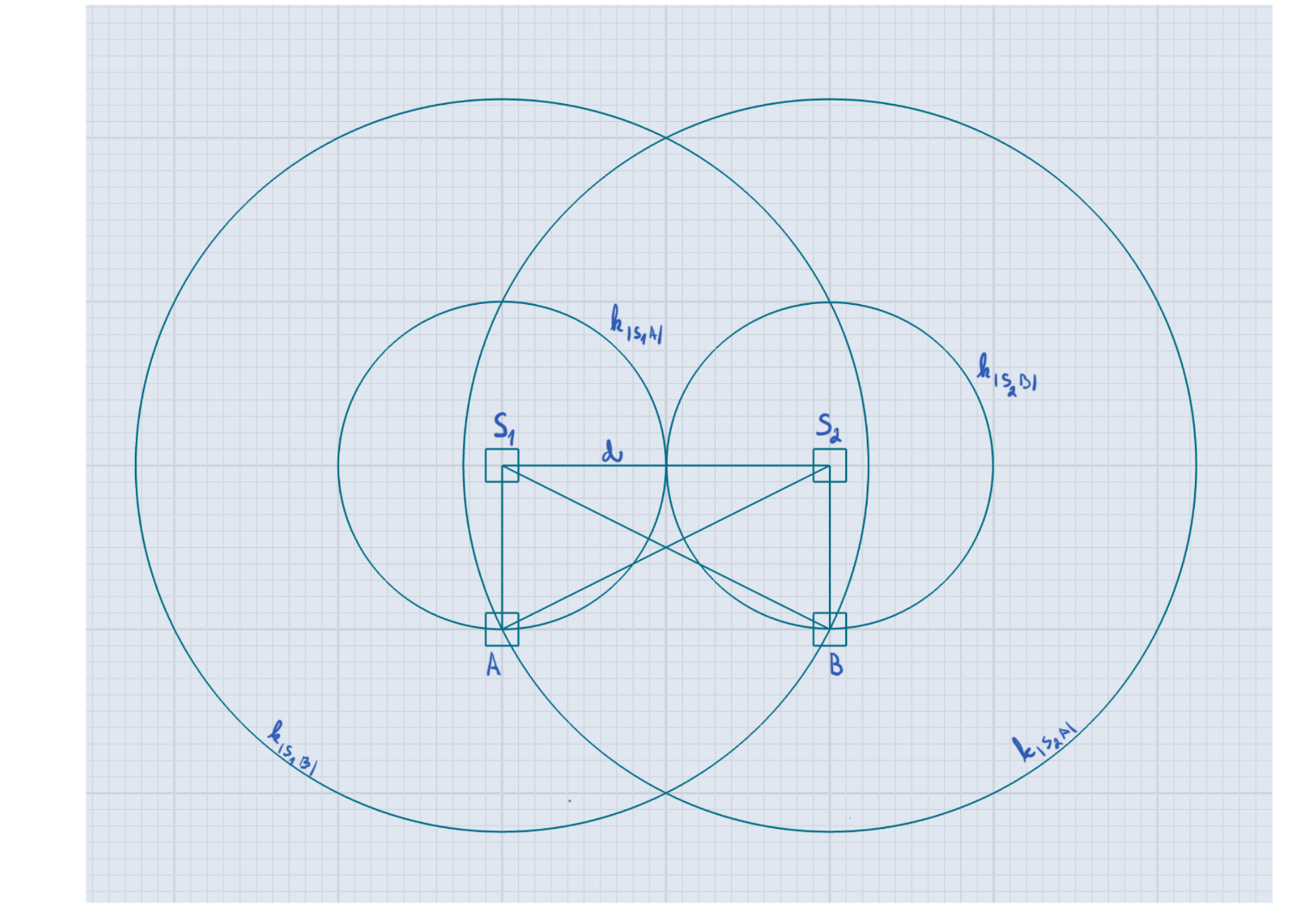
We send 2 QUERY messages from each controller. $S_1$ sets HOPS_TO_GO to
translation of the distance $|S_1 A|$. The distances $|S_1 B|, |S_2 A|, |S_2
B|$ correspond to one message each. UNION is set to 2 for all messages,
because we expect intersection of 2 circles in both A and B.
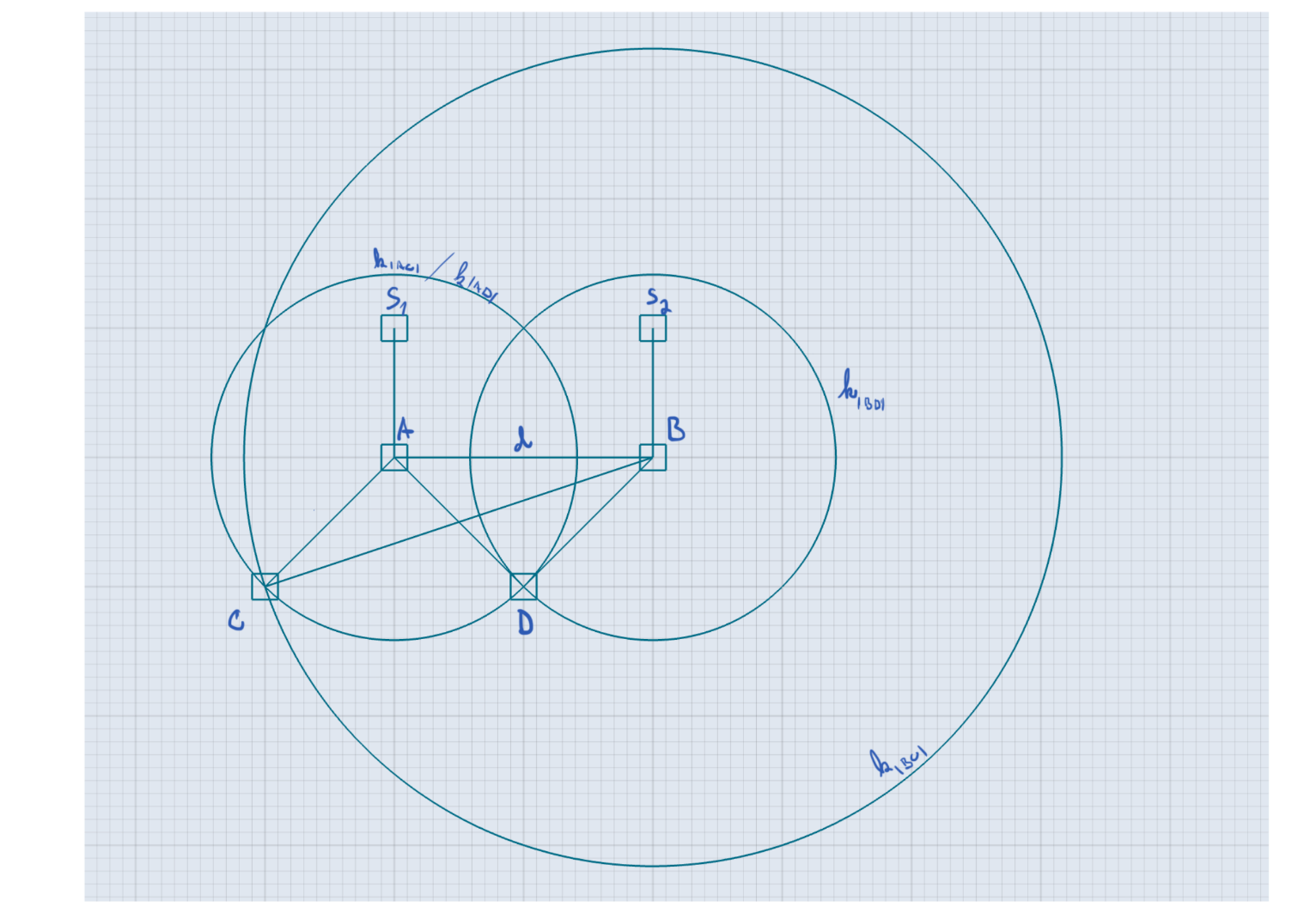
The TAIL parameter allows us to recursively unfold the QUERY. After
localizers in A and B receive the messages, they read the TAIL parameter
containing instructions for another QUERY message which leads to points C and
D. In the example we set HOPS_TO_GO to target points C and D under an angle.
Using this technique our QUERY message can navigate known space even though a
single localizer posses no information about its own position3. Extending
this technique to 3-space $S$ we can navigate around $O$, thereby reading
sensory information of localizers positioned behind $O$4.
Estimating localizer density
We solve a situation in which we don’t know the number of localizers upfront. A
localizer periodically broadcasts PING message to its peers. The message
contains ORIGIN id and HOPS counter. We promote the set of recently relayed
ORIGIN ids to a map between an ORIGIN and a timestamp (let’s assume our
localizers posses some sort of clock). A localizer can estimate current load of
the network around it. Let’s denote this as NETWORK_LOAD variable.
A localizer remembers the last time it sent a PING message. Let’s denote
this as SINCE_LAST_PING variable. A decision function for broadcasting
PING accepts SINCE_LAST_PING and NETWORK_LOAD and yields a
boolean. Each localizer performs this computation in some interval.
By listening to the network, we can track a path taken by some subset of localizers through the space, which is useful if we know that those localizers are attached to an object of interest.
A major issue with periodic PING is deploying it on scale. Say we have a
space of size of a cargo container uniformly filled with localizers which are
~0.5mm apart. To fill the volume of $50m^3$ we would need 100k localizers. Say
the frequency of a PING event should ideally be 10s. That results in 10k
new messages broadcasted to neighbours every second. The LOAD variable
should throttle messages in a busy network, right? Yes, the network will auto
adjust the periodicity of the PING message, but the periodicity only depends
on the density and what a localizer considers high LOAD There’s no
guarantee the throttling will result in a reasonable periodicity.
To lower the periodicity of PING messages from the same localizer, we can
further limit hops by a constant MAX_HOPS. Therefore we can at least estimate
density in the proximity of MAX_HOPS from the controllers. Further
investigation on the behavior of periodic messages in the network is necessary.
-
Not always accurate. Displaced localizers create areas of different densities, effectively skewing distances. The message might need to travel around an obstacle, bending the path of the “shock wave”. Further investigation of these situations is necessary. ↩︎
-
The problem of positioning the controllers is hard. In the hello world environment $S$ positioning the controllers near each other into one plane works. However, we will need to rethink the approach when we try to model more interesting scenarios. ↩︎
-
There is a problem of mirror images of A, B, C and D. The same problem plagues other algorithms and is a consequence of individual localizers not being aware of spacial dimensions. ↩︎
-
A problem to consider is the two parallel pathways drifting out of sync as the recursion unfolds. For this we could introduce a syncing message
QUERY_SYNC, which should be fairly trivial as we know the distance between A and B, C and D, and so on. ↩︎
